Data Structures

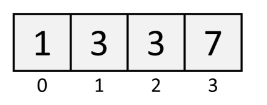
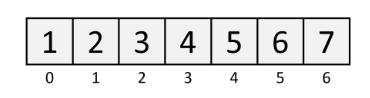
Array

arr = [1, 3, 3, 7]

for val in arr:
    # 1,3,3,7

7 in arr         # True, takes O(n)

arr[3]           # 7
arr[3] = 8
arr.pop()        # delete last element
arr.append(9)    # insert last element

del arr[1]       # delete, takes O(n)
arr.insert(1, 9) # insert, takes O(n)

An Array is an ordered list of elements. Each element in an Array exists at an index 0, 1, 2, and so on.

Arrays are called "lists" in Python.

Lists can have duplicate values

Read/Write Time O(1).
Insert/Delete Time O(n).

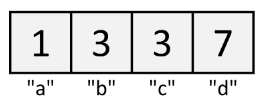
Hashmap

HashMaps are Arrays, but where you can look up values by string, tuple, number, or other data, called a "key".

HashMaps are called "dictionaries" or "dicts" in Python.

We talk about how to implement a HashMap from scratch here.

h = {} # empty hashmap
h = { # hashmap of the above image
    "a": 1,
    "b": 3,
    "c": 3,
    "d": 7
}

# look for a key, and if it doesn't exist, default to 0
h.get("a", 0) # 1
h.get("e", 0) # 0

for key in h: 
    print(key) # "a" "b" "c" "d"

for k,v in h.items(): 
    print(k) # "a" "b" "c" "d"
    print(v) # 1 3 3 7

h["b"]         # read value (3)
h["b"] = 9     # write value (9)
del h["b"]     # delete value

"a" in h # True, O(1)

Keys have to be unique

Read/Write Time O(1).

Insert/Delete Time O(1).

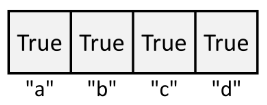
Set

Sets are essentially HashMaps where all the values are True. Python implements them as a new data structure for convenience.

Sets let you quickly determine whether an element is present. Here's the syntax for using a Set.

s = set() # empty set
s = {"a", "b", "c", "d"} # set of the above image

s.add("z")     # add to set
s.remove("c")  # remove from set
s.pop()        # remove and return an element

for val in s:
    print(val) # "a" "b" "d" "z"

"z" in s # True, O(1)

Read/Write Time O(1).

Add/Remove Time O(1).

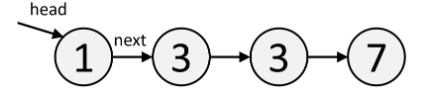
Linked List

A Linked List is a custom data structure that you implement yourself. The first node in the Linked List is called the "head". Each node has a value val, and points to the next node next.

# create nodes, and change next pointers
head = ListNode(1)
b    = ListNode(3)
c    = ListNode(3)
d    = ListNode(7)
head.next = b
b.next    = c
c.next    = d

# you can also create the list using the ListNode(val, next) function
head = (
    ListNode(1,
        ListNode(3,
            ListNode(3, ListNode(7))
        )
    )
)

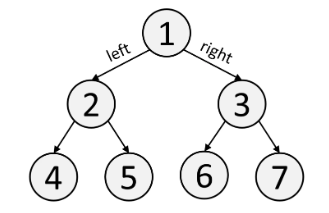
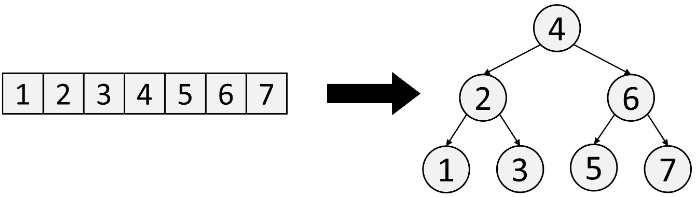
Tree

Trees are a custom data structure you implement yourself. Usually, "Tree" means Binary Tree. In a Binary Tree, each node has a value val, a left child left, and a right child right.

# you can create the above tree by creating TreeNode objects
root = TreeNode(1)
l    = TreeNode(2)
r    = TreeNode(3)
ll   = TreeNode(4)
lr   = TreeNode(5)
rl   = TreeNode(6)
rr   = TreeNode(7)
root.left  = l
root.right = r
l.left     = ll
l.right    = lr
r.left     = rl
r.right    = rr

# an easier way to write that code is to nest TreeNodes
root = TreeNode(1,
    TreeNode(2,
        TreeNode(4),
        TreeNode(5)
    ),
    TreeNode(3,
        TreeNode(6),
        TreeNode(7)
    )
)

Trees generally have a height of O(n), but balanced trees are spread wider and have a height of O(log n), which makes reading/writing faster.

Read/Write Time O(n).

Read/Write Time O(log n) for balanced trees like Binary Search Trees and Heaps.

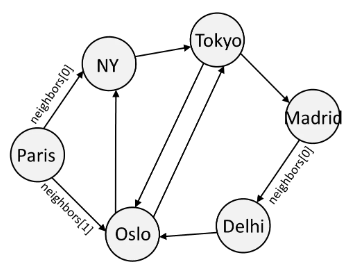
Graph

A graph is made of nodes that point to each other.

There are two ways you can store a graph. It doesn't matter which one you pick.

# Option 1: create nodes, and point every node to its neighbors
Paris = Node()
NY    = Node()
Tokyo = Node()
Madrid= Node()
Delhi = Node()
Oslo  = Node()
Paris.neighbors = [NY, Oslo]
NY.neighbors    = [Tokyo]
Tokyo.neighbors = [Madrid, Oslo]
Madrid.neighbors= [Delhi]
Delhi.neighbors = [Oslo]
Oslo.neighbors  = [NY, Tokyo]

# Option 2: create an "Adjacency Matrix" that stores all the connections
adjacenyMatrix = {
    'Paris': ['NY', 'Oslo'],
    'NY':    ['Tokyo'], 
    'Tokyo': ['Madrid', 'Oslo'],
    'Madrid':['Delhi'],
    'Delhi': ['Oslo'],
    'Oslo':  ['NY', 'Tokyo'],
}

Read/Write Time Varies.

Insert/Delete Time Varies.

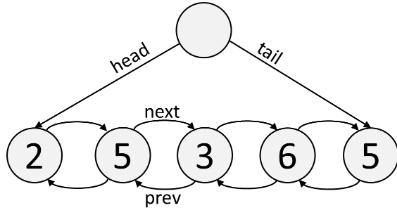
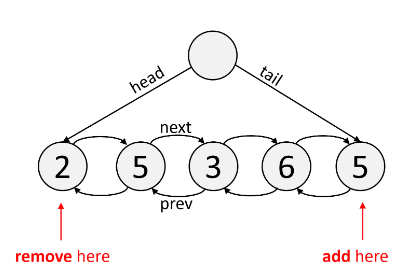
DeQueue (Double-Ended)

A Double-Ended Queue (Deque) is a Linked List that has pointers going both ways, next and prev. It's a built-in data structure, and the syntax is similar to an Array.

The main benefit of Deques is that reading and writing to the ends of a Deque takes O(1) time.

The tradeoff is that reading and writing in general takes O(n) time.

from collections import deque
dq = deque([2, 5, 3, 6, 5])

# These are O(1)
dq.pop()           # remove last element
dq.popleft()       # remove first element
dq.append("a")     # add last element
dq.appendleft("b") # add first element

#These are O(n)
dq[3]
dq[3] = 'c'

for val in dq:
    print(val) # 2 5 3 6 5

5 in dq # True, takes O(n)

Read/Write Time O(n).

Insert/Delete Time O(n).

Append/Pop Time O(1).

AppendLeft/PopLeft Time O(1).

Queue 

A Queue adds elements from one side, and remove elements from the opposite side. This means you remove elements in the order they're added, like a line or "queue" at grocery store. Typically you add to the right and pop from the left.

You can implement a Queue using a Deque, or implement it yourself as a custom data structure.

from collections import deque
q = deque([1, 3, 3, 7])

val = q.popleft() # remove 0th element
print(val)        # 1
print(q)          # [3, 3, 7]

q.append(5)       # add as last element
print(q)          # [3, 3, 7, 8, 5]

Read/Write Time O(1).

Append/Pop Time O(1).

Sorted Array

A Sorted Array is just an Array whose values are in increasing order.

Sorted Arrays are useful because you can use Binary Search, which takes O(log n) time to search for an element. Here are some built-in Python methods for sorting an Array.

# sorted() creates a new sorted array:
array = sorted([4,7,2,1,3,6,5])

# .sort() modifies the original array:
array2 = [4,7,2,1,3,6,5]
array2.sort()

print(array)  # [1,2,3,4,5,6,7]
print(array2) # [1,2,3,4,5,6,7]

Python's bisect library contains Binary Search methods you can use, although often you'll have to implement Binary Search yourself in an interview.

Search Time O(log n).

Insert/Delete Time O(n).

Sort Time O(n log n).

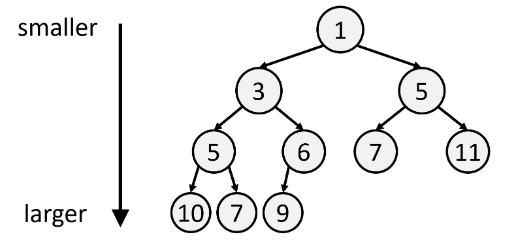
Binary Search Tree

A Binary Search Tree (BST) is just a Sorted Array but in tree form, so that inserting/deleting is faster than if you used a Sorted Array. It's a custom data structure - there is no built-in BST in Python.

Stepping left gives you smaller values, and stepping right gives you larger values. A useful consequence of this is that an inorder traversal visits values in a BST in increasing order.

Search Time O(log n).

Insert/Delete Time O(log n).

Create Time O(n log n).

Heap

A Heap is a Tree, where the values increase as you step downwards.

The purpose of a Heap is to have immediate access to the smallest element.

The smallest element is always at the top. Heaps are always balanced, and they're stored as Arrays in the order of their BFS traversal. We introduced Heaps here.

import heapq
h = [5,4,3,2,1]
heapq.heapify(h)     # turns into heap, h=[1,2,3,5,4]
h[0]                 # find min

heapq.heappop(h)     # h=[2,4,3,5]
heapq.heappush(h, 3) # h=[2,3,3,5,4]
h[0]                 # find min

Python only allows Min-Heaps (smallest values on top). If you want a Max-Heap, you can implement it with a Min-Heap by negating all your values when you push and pop.

Read Time O(1).

Push/Pop Time O(log n).

Create Time O(n).