Big O
How should we describe the speed of an algorithm? One idea is to just count the total number of
primitive operations it does (read, writes, comparisons) when given an input of size n. For example:
The thing is, it's hard to come up with a formula like this, and the coefficients will vary based on what
processor you use. To simplify this, computer scientists only talk about how the algorithm's speed
scales when n gets very large. The biggest-order term always kills the other terms when n gets very
large (plug in n=1,000,000). So computer scientists only talk about the biggest term, without any
coefficients. The above algorithm has n3 as the biggest term, so we say that:
Time Complexity = O(n3 )
Verbally, you say that the algorithm takes "on the order of n3 operations". In other words, when n gets
very big, we can expect to do around n3 operations.
Computer scientists describe memory based on how it scales too. If your progam needs 51n2 + 200n
units of storage, then computer scientists say Space Complexity = O(n2 ).
Time ≥ Space
The Time Complexity is always greater than or equal to the Space Complexity. If you build a size
10,000 array, that takes at least 10,000 operations. It could take more if you reused space, but it can't
take less - you're not allowed to reuse time (or go back in time) in our universe.

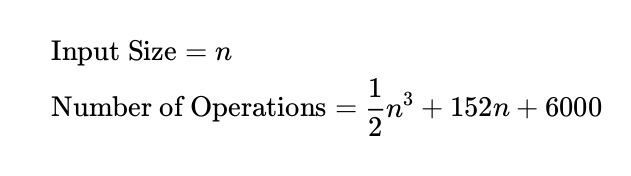
No Comments