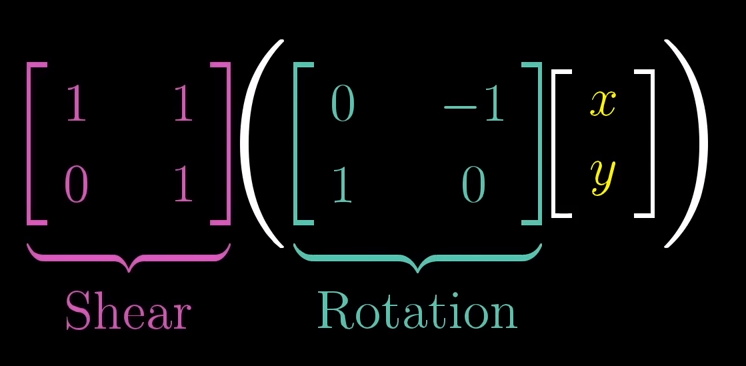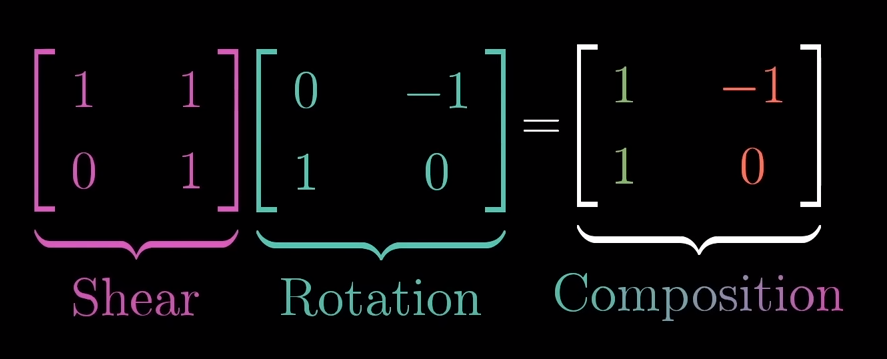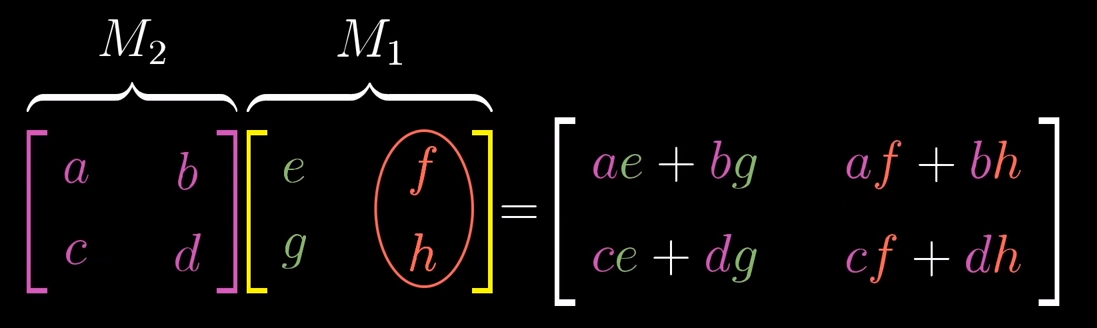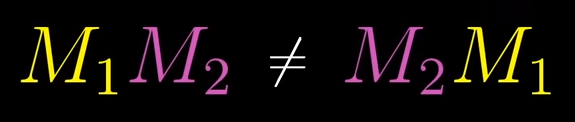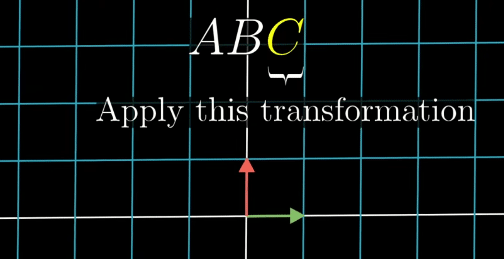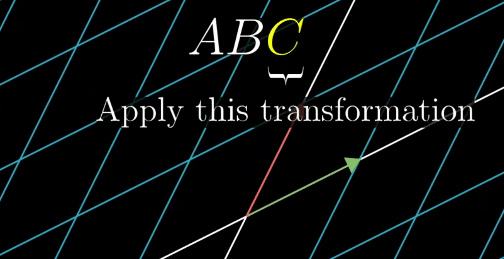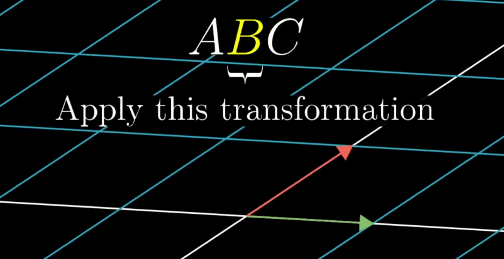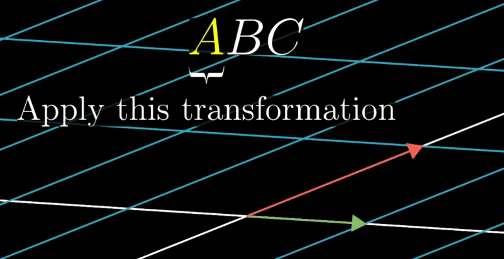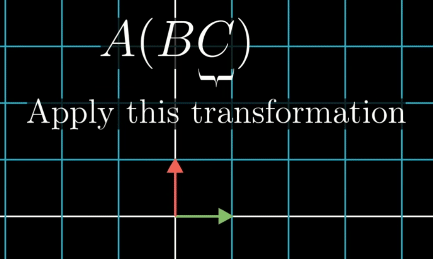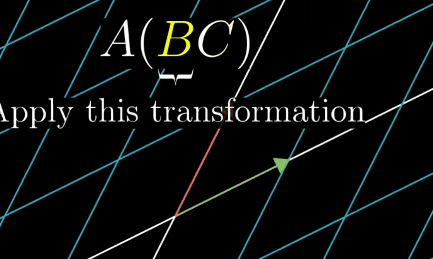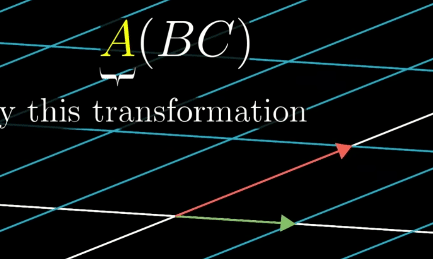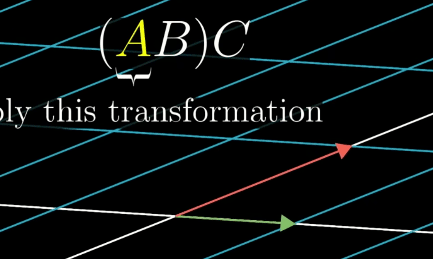Matrix multiplication and Composition
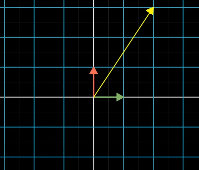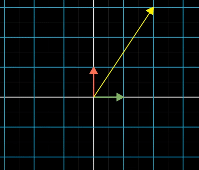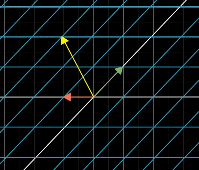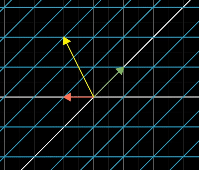
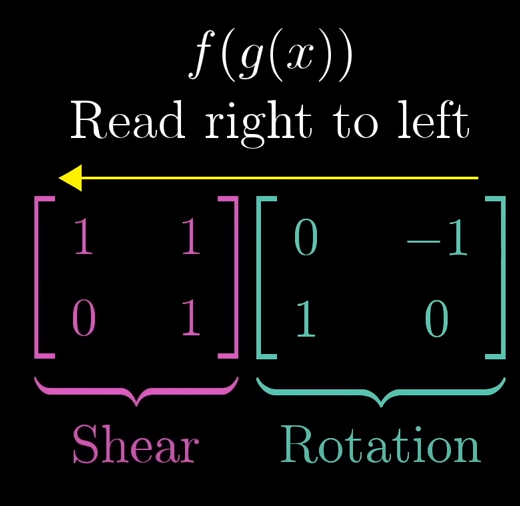
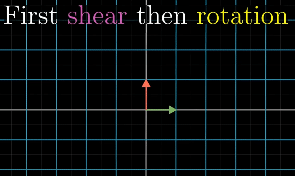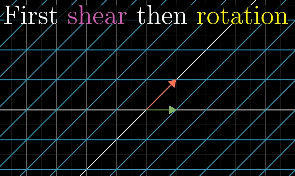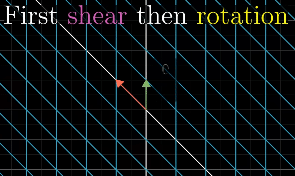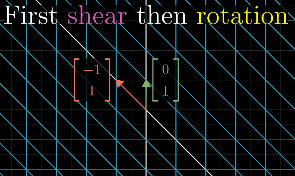
In order to describe the effects of multiple sequential matrix transformation, such as a rotate and then a shear, we use matrix multiplication on those individual matrices to create a new matrix, called composition, to perform the action at once.
MatrixOrder Multiplicationof isthe AssociativeMatrices matter
The isfollowing associative, meaningdemonstrates that parentheses does not matter,if the pattern will still have the same result as long as the right to left order is reversed, the samevector
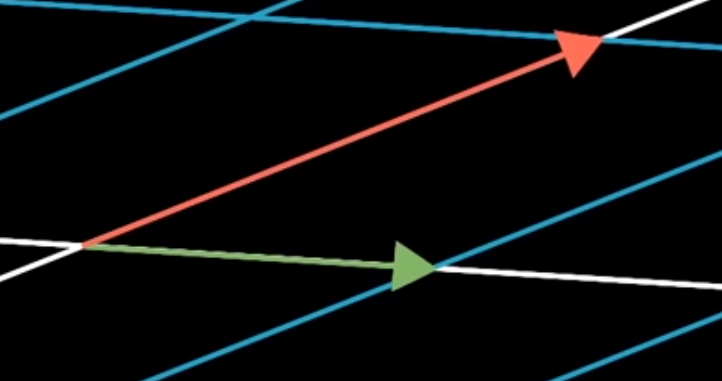
Matrix Multiplication is Associative
Also this is associative, meaning that parentheses does not matter, the pattern will still have the same result as long as the right to left order is the same
End result will always look the same