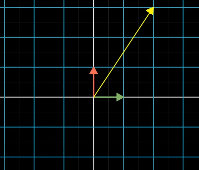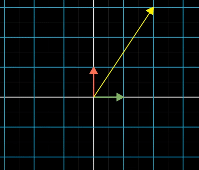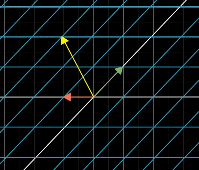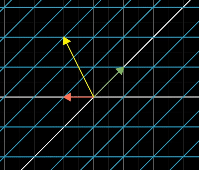
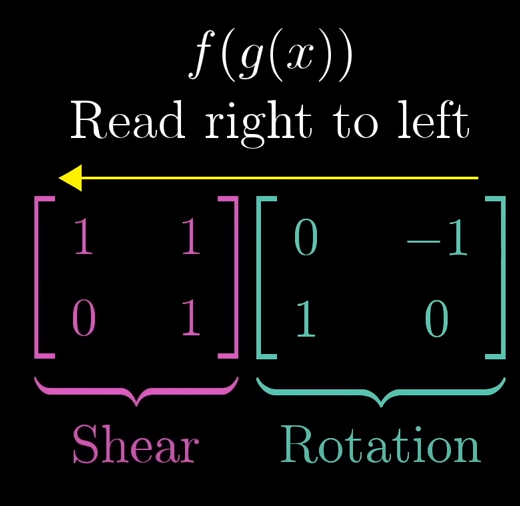
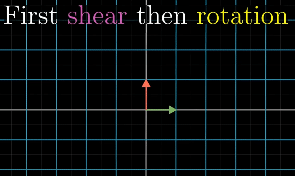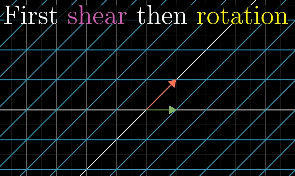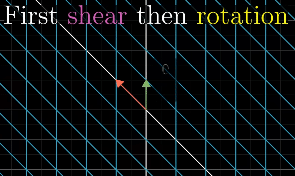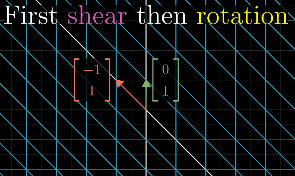
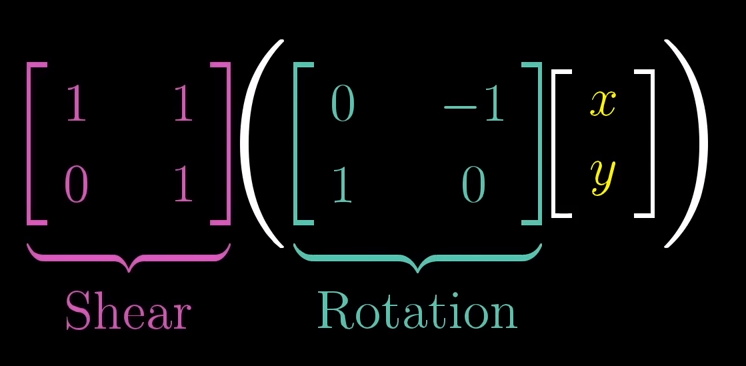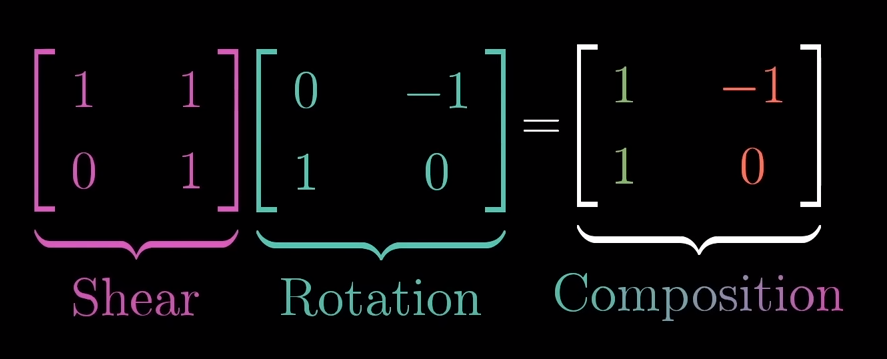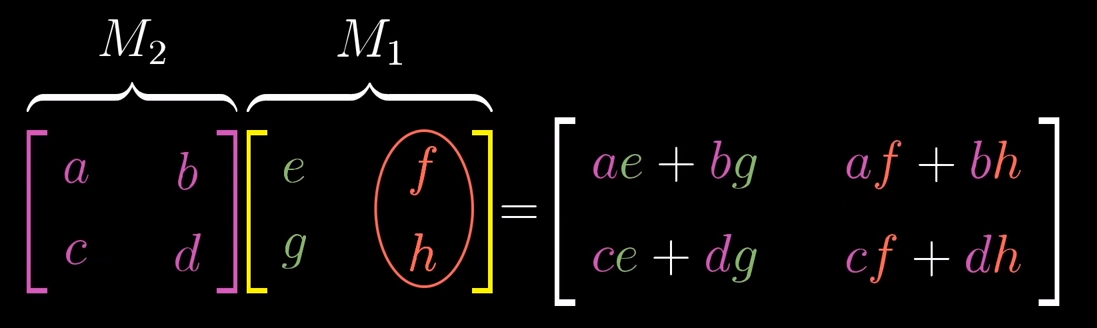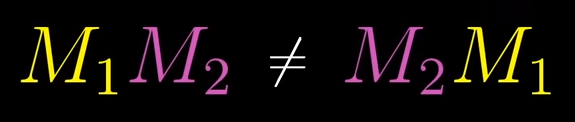Skip to main content

Matrix multiplication and Composition

In order to describe the effects of multiple sequential matrix transformation, such as a rotate and then a shear, we use matrix multiplication on those individual matrices to create a new matrix, called composition, to perform the action at once. 

IBQmm-matrix-rotation-then-shear.gif

image.pngimage.png

image.png

 

image.png

MM_matrix-multiplication-example.gif

 

image.png

MM_matrix-shear-then-rotate.gif

MM_matrix-rotate-then-shear.gif

Back to top