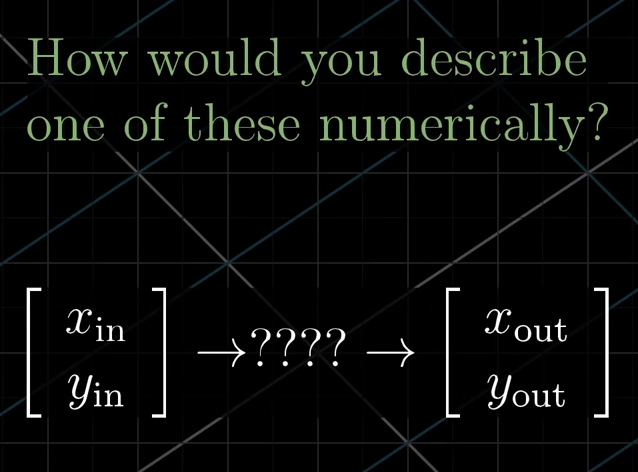Linear Transformations

Linear Transformation of Matrices

Prereq knowledge: Vectors and Basis Vectors, Linear dependent and independent 

Linear Transformation is a way to move around space such that it fulfills these two conditions: 

1. All grid lines must remain lines 
2. Origin (0,0) must remain fixed 

Transformations (functions f(x) - best described as a movement from input to its output)

The following are Linear Transformation where the grey grid is the original:

 

 

The following are Non Linear Transformations

---

 

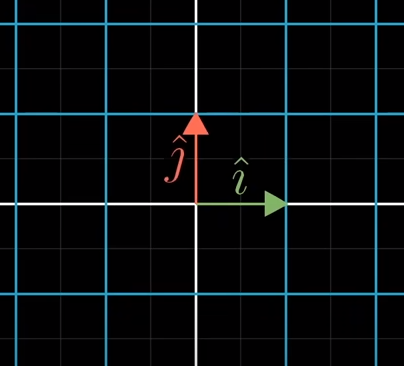
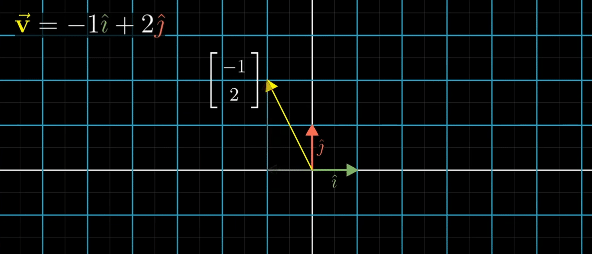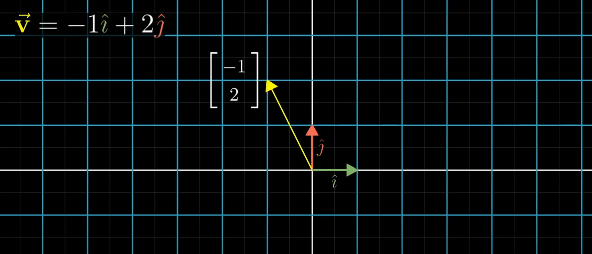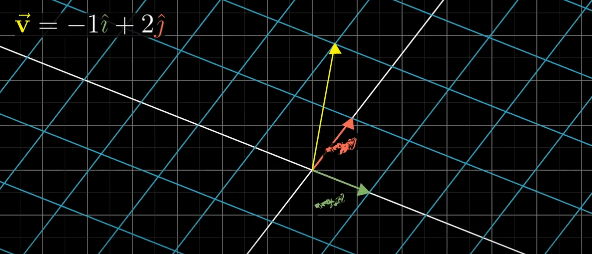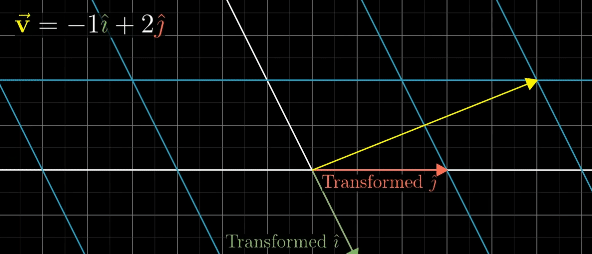
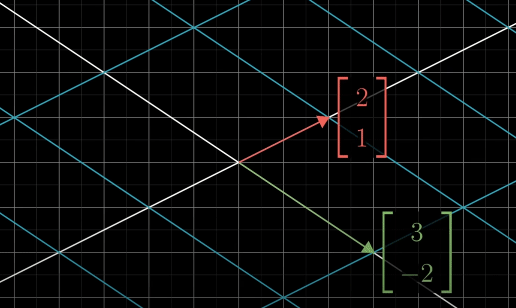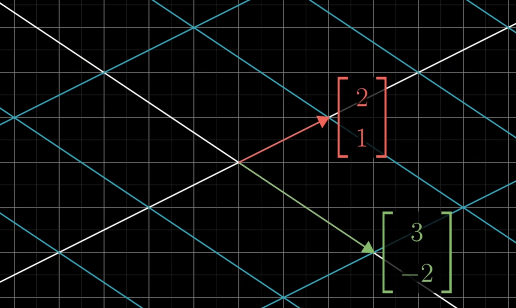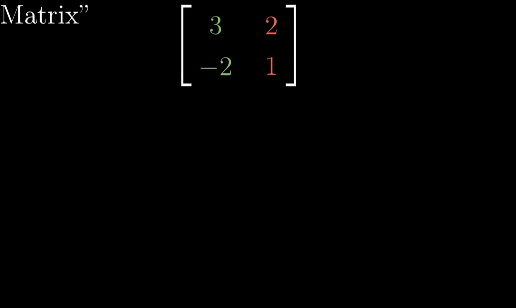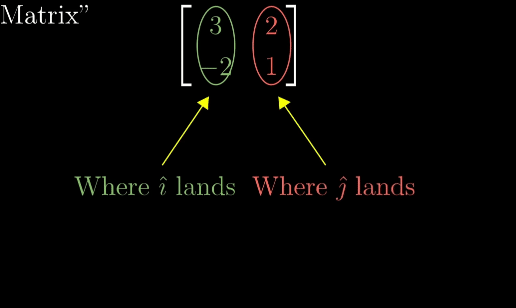
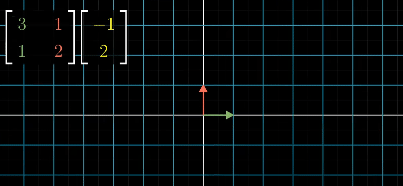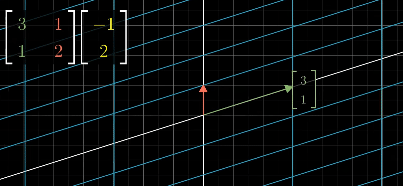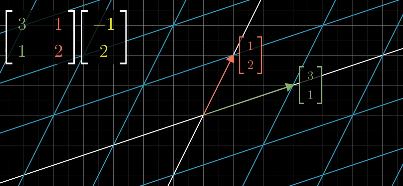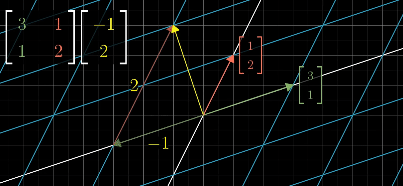
With the above two conditions are fulfilled, we can deduce where ANY vector land as long as we have record of where i hat and j hat lands. In 2D space, this only requires two vectors 

Example of i hat and j hat moving to their new space based on the formula (linear combination?)

A 2x2 Matrix is created through two vectors

The columns in the matrix are transformed versions of the basis vectors,  and the result is the linear combination of those vectors

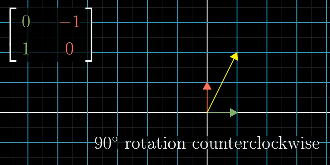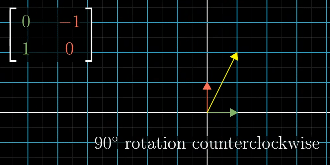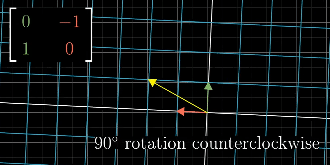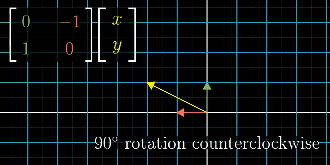
example of a 90 degree rotation counter clockwise matrix applied to a vector in yellow 

When you see a matrix, it is interpreted as a certain transformation in space.

You need to use matrix operations in order to do transformations, like Rotate Shear and Scale for matrix multiplication and translation and reflection for matrix addition. 

Matrices can encode geometric operations such as rotation, reflection and transformation. Thus if a collection of vectors represents the vertices of a three-dimensional geometric model in Computer Aided Design software then multiplying these vectors individually by a pre-defined rotation matrix will output new vectors that represent the locations of the rotated vertices. This is the basis of modern 3D computer graphics. 

An affine transformation is a combination of linear transformations (such as translation, rotation, scaling, and shearing) and a translation (a constant vector addition). Affine transformations preserve straight lines and parallelism, and they map collinear points to collinear points.

Matrix-Matrix Multiplication

Transformations

Rotate

uses sin/cos in trig

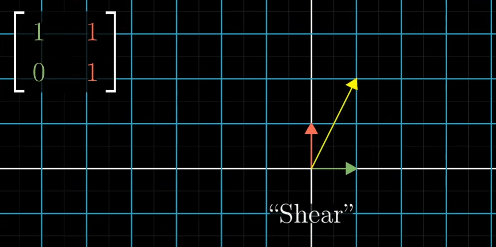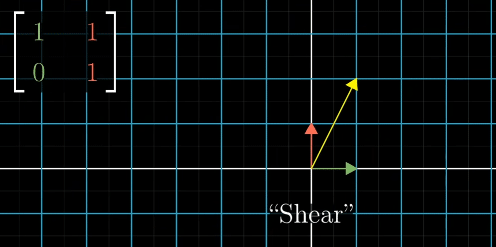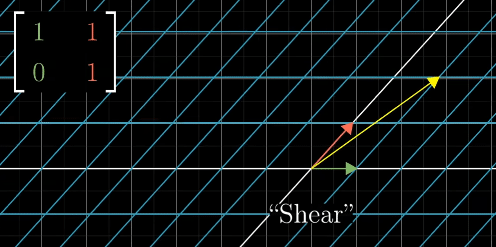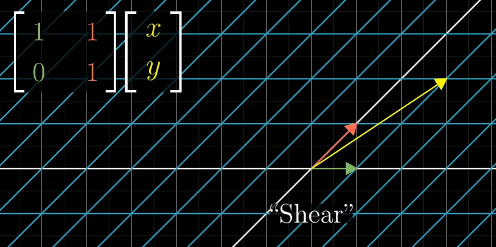
Shear 

Scaling

Matrix Addition

Matrix-Scalar Addition 

Matrix-Matrix Addition

Needed for Translation of a vector 

Matrix addition is commutative. This means that it doesn't matter which way around the matrices are added:

�+�=�+�

It is also associative. This means that you get the same result if you add two matrices together first, and then another, as if you add another two together first and then the other:

�+(�+�)=(�+�)+�

Both of these results follow from the fact that normal scalar addition is itself commutative and associative, because we're just adding the elements together.

Matrix Multiplication

Matrix Transpose

Scalar-Matrix Multiplication

Hadamard Product

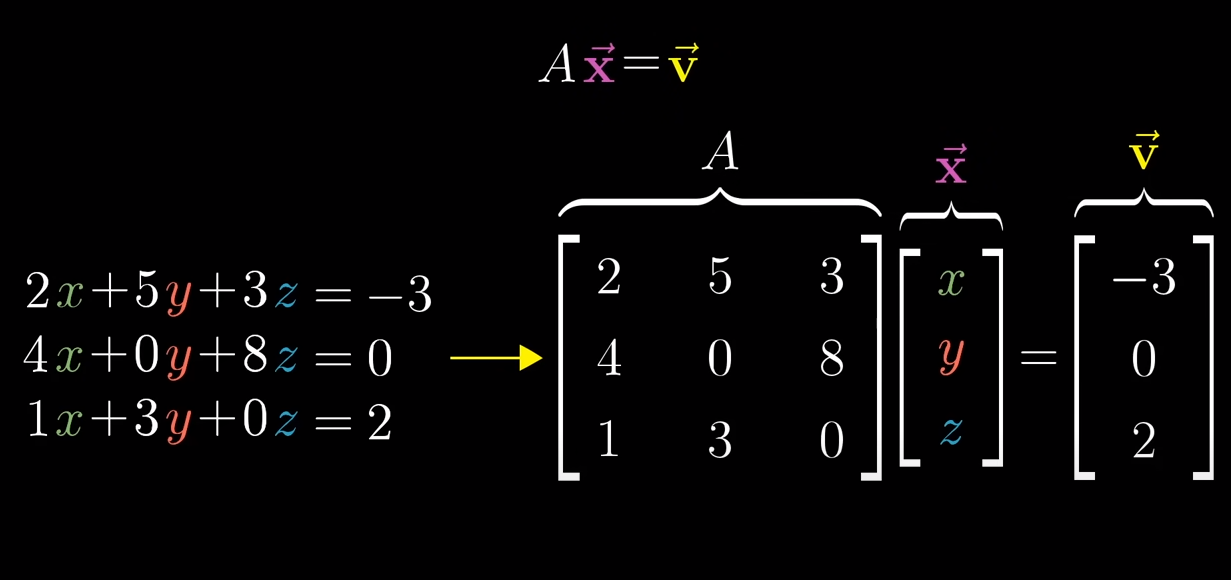
Linear Systems of Equations

can be converted to martrix math