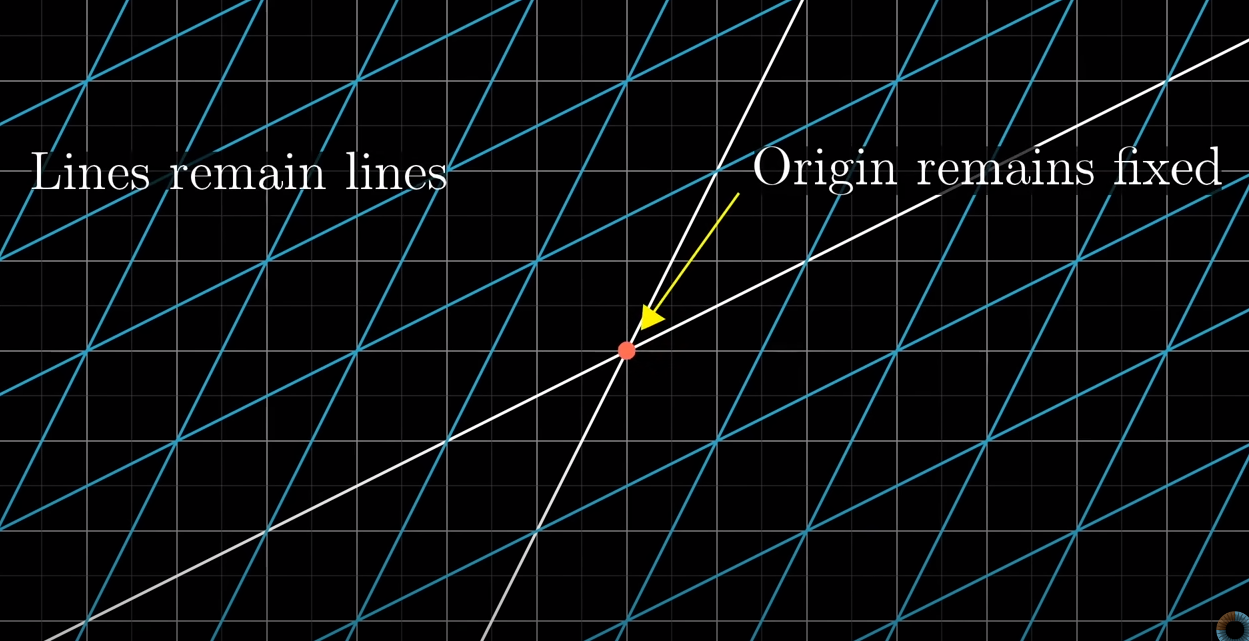
Linear Transformations
Definition
Prereq knowledge: Basis Vectors
Matrices are essentially transformation of space.
Lineaer Transformations abide by 2 rules
with the grey grid being the input, and purple grid as the output.
Matrices can encode geometric operations such as rotation, reflection and transformation. Thus if a collection of vectors represents the vertices of a three-dimensional geometric model in Computer Aided Design software then multiplying these vectors individually by a pre-defined rotation matrix will output new vectors that represent the locations of the rotated vertices. This is the basis of modern 3D computer graphics.
Matrix-Matrix Multiplication
Transformations
Rotate
Shear
Scaling
Matrix Addition
Matrix-Scalar Addition
test
Matrix-Matrix Addition
Needed for Translation of a vector
Matrix addition is commutative. This means that it doesn't matter which way around the matrices are added:
�+�=�+�
It is also associative. This means that you get the same result if you add two matrices together first, and then another, as if you add another two together first and then the other:
�+(�+�)=(�+�)+�
Both of these results follow from the fact that normal scalar addition is itself commutative and associative, because we're just adding the elements together.