Linear Transformations

Definition

IfPrereq knowledge: Basis Vectors

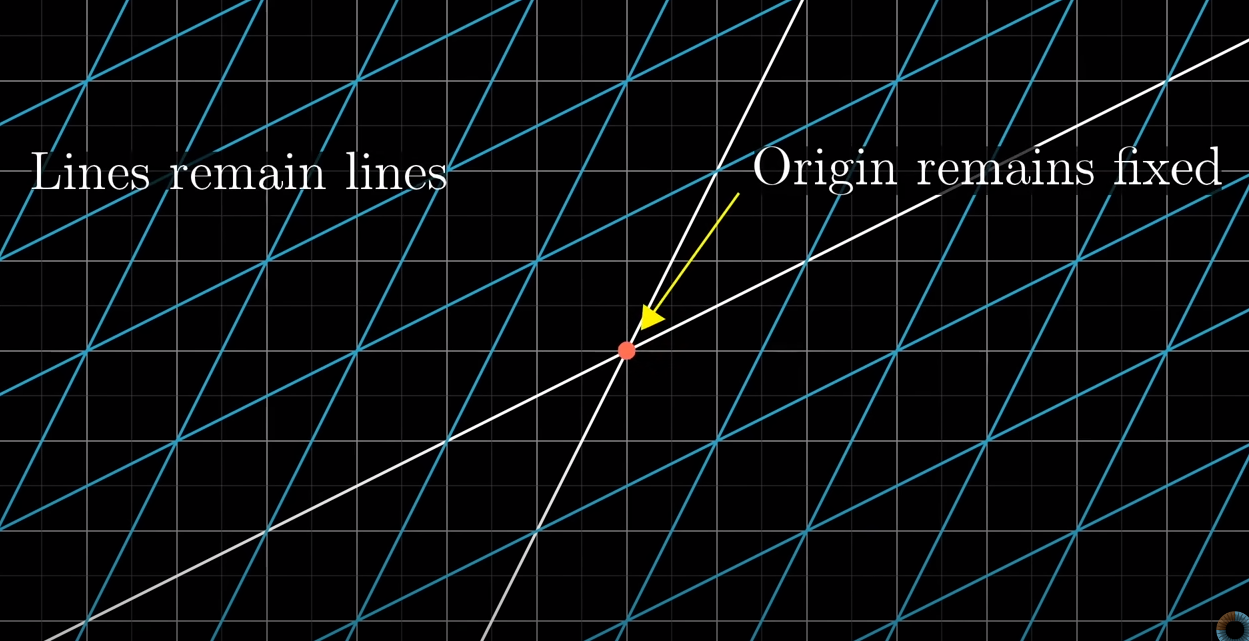
Matrices are essentially transformation of space. 

Lineaer Transformations abide by 2 rules

with the operationgrey preservesgrid vectorbeing additionthe input, and scalarpurple multiplication,grid itas the output. 

 

Matrices can beencode viewedgeometric operations such as arotation, linear transformation,reflection and matricestransformation. associatedThus withif sucha operationscollection areof oftenvectors usedrepresents tothe vertices of a three-dimensional geometric model in Computer Aided Design software then multiplying these vectors individually by a pre-defined rotation matrix will output new vectors that represent linearthe transformations.locations of the rotated vertices. This is the basis of modern 3D computer graphics.

Matrix-Matrix Multiplication

Transformations

To be considered a linear transformation, a matrix operation must satisfy two fundamental properties: additivity and homogeneity.Rotate

AShear linear transformation $T:V\to W$ between vector spaces $V$ and $W$ must satisfy the following for all vectors $u$ and $v$ in $V$ and scalars $c$:

1. Scaling

   Additivity: $T(u+v)=T\left(u\right)+T\left(v\right)$

2. Homogeneity: $T\left(cu\right)=cT\left(u\right)$

Matrix Addition

Matrix-Scalar Addition 

test

Matrix-Matrix Addition

Matrix Multiplication

Matrix Transpose

Matrix-Matrix Multiplication

Scalar-Matrix Multiplication

Hadamard Product