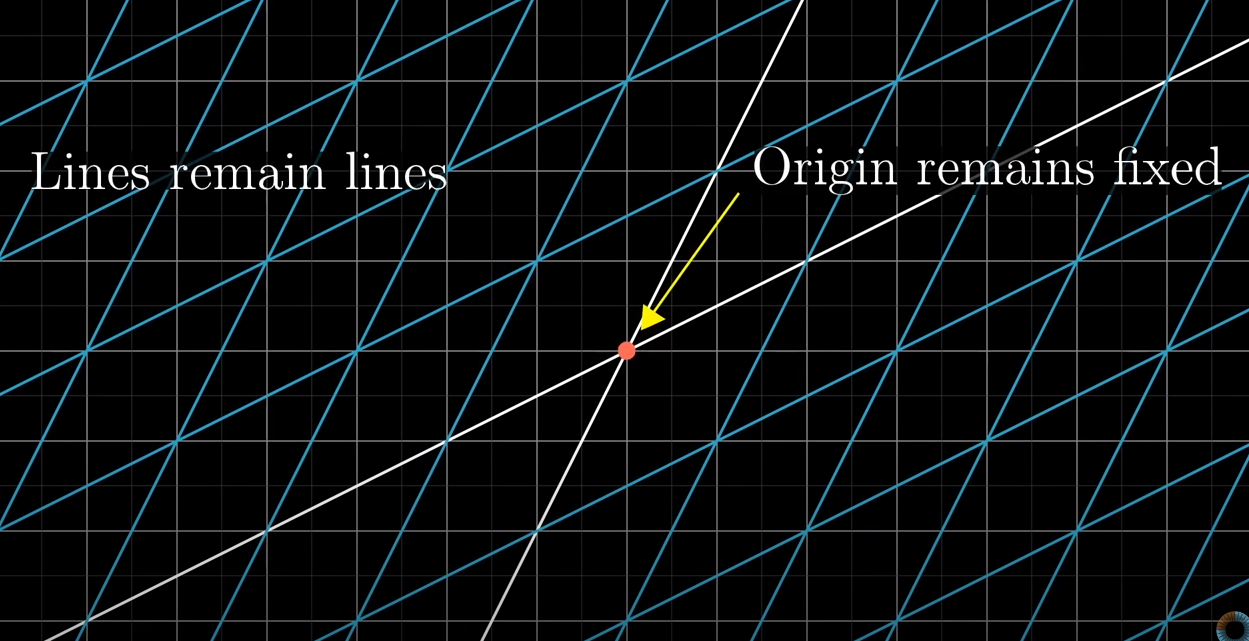
Linear Transformations
Definition
Prereq knowledge: Basis Vectors
Matrices are essentially transformation of space.
Lineaer Transformations abide by 2 rules
with the grey grid being the input, and purple grid as the output.
Matrices can encode geometric operations such as rotation, reflection and transformation. Thus if a collection of vectors represents the vertices of a three-dimensional geometric model in Computer Aided Design software then multiplying these vectors individually by a pre-defined rotation matrix will output new vectors that represent the locations of the rotated vertices. This is the basis of modern 3D computer graphics.
Matrix-Matrix Multiplication
Transformations
Rotate
Shear
Scaling
Matrix Addition
Matrix-Scalar Addition
test