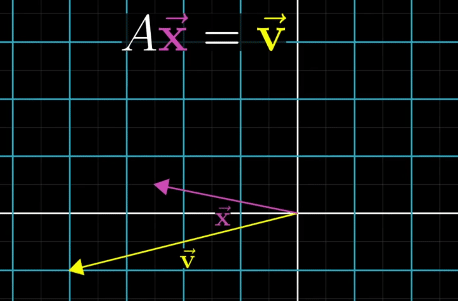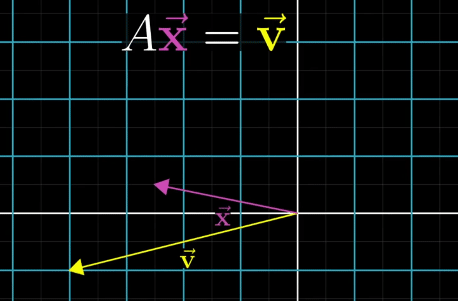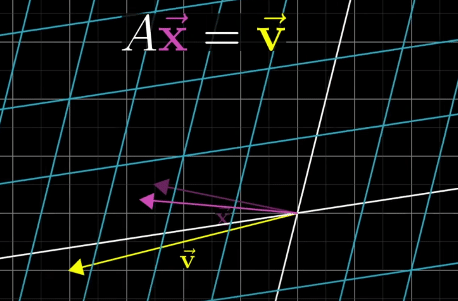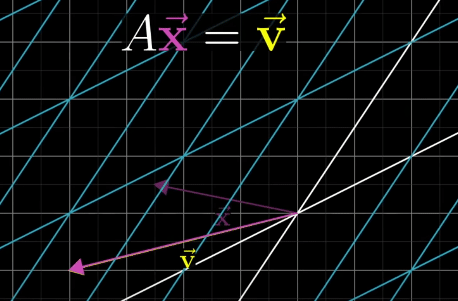
Linear System of Equations
A system of equations consists of unknown variables and list of equations relating them.
A Linear System of Equations fulfill the following:
- The list of variable (xyz) is scaled by some constant number
- The only thing happening to each variable is that they are added to each other
- no exponents, no multiplication, no sin/cos/tan or other special functions
A Linear System of Equations is organized by putting scaled variables on the left and constants on the right. Also add Zeros to variables if not present.
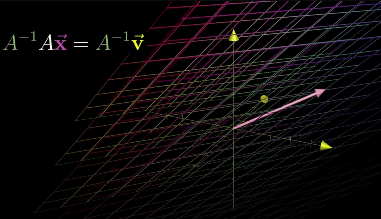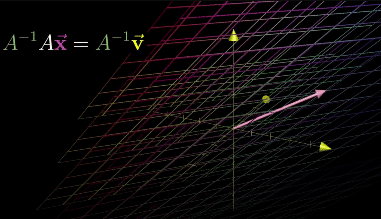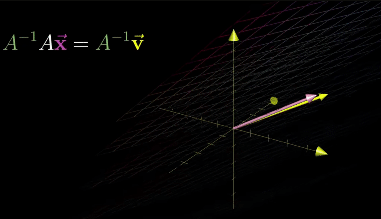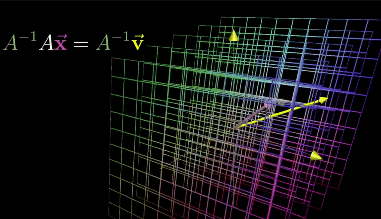
A Linear System of Equations can be transferred to a vector equation with following equation, where A is the matrix holding all the constant coefficients.
Computers used matrices because its more efficient than linear system of equations
ide
Inverse Transformation
Prereq: Determinant
identity matrix:
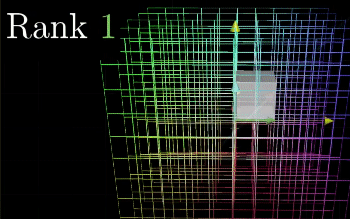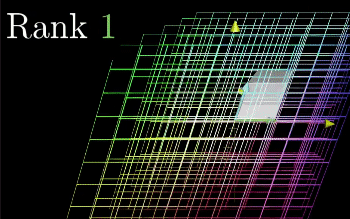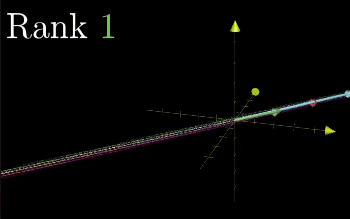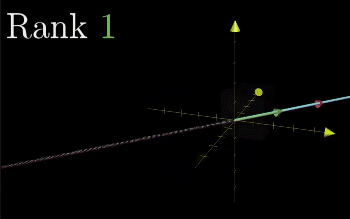
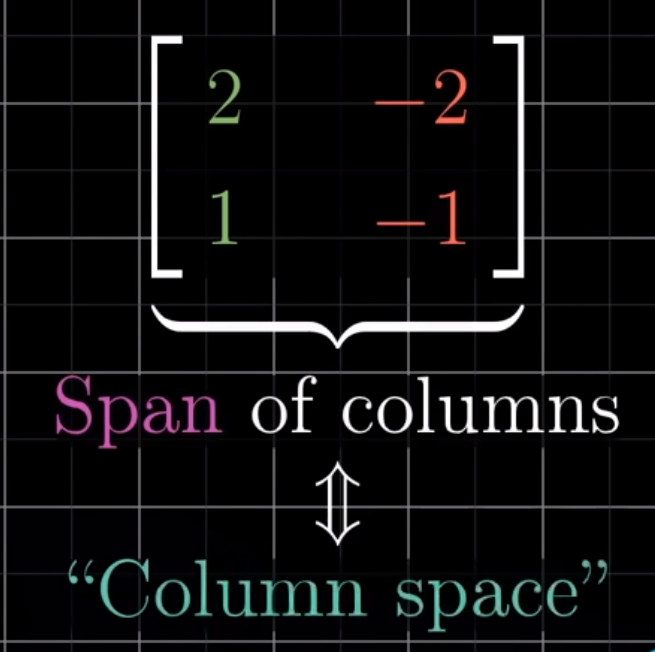
Rank = Number of Dimensions in the Column Space
When the column space equals the number of columns, it is Full Rank. The following example is Full Rank
When determinant is 0, we can use Rank to describe the number of dimensions in the output of the transformation
Null Space (Kernel) is the space of all vectors that land on Null (0 Vector).

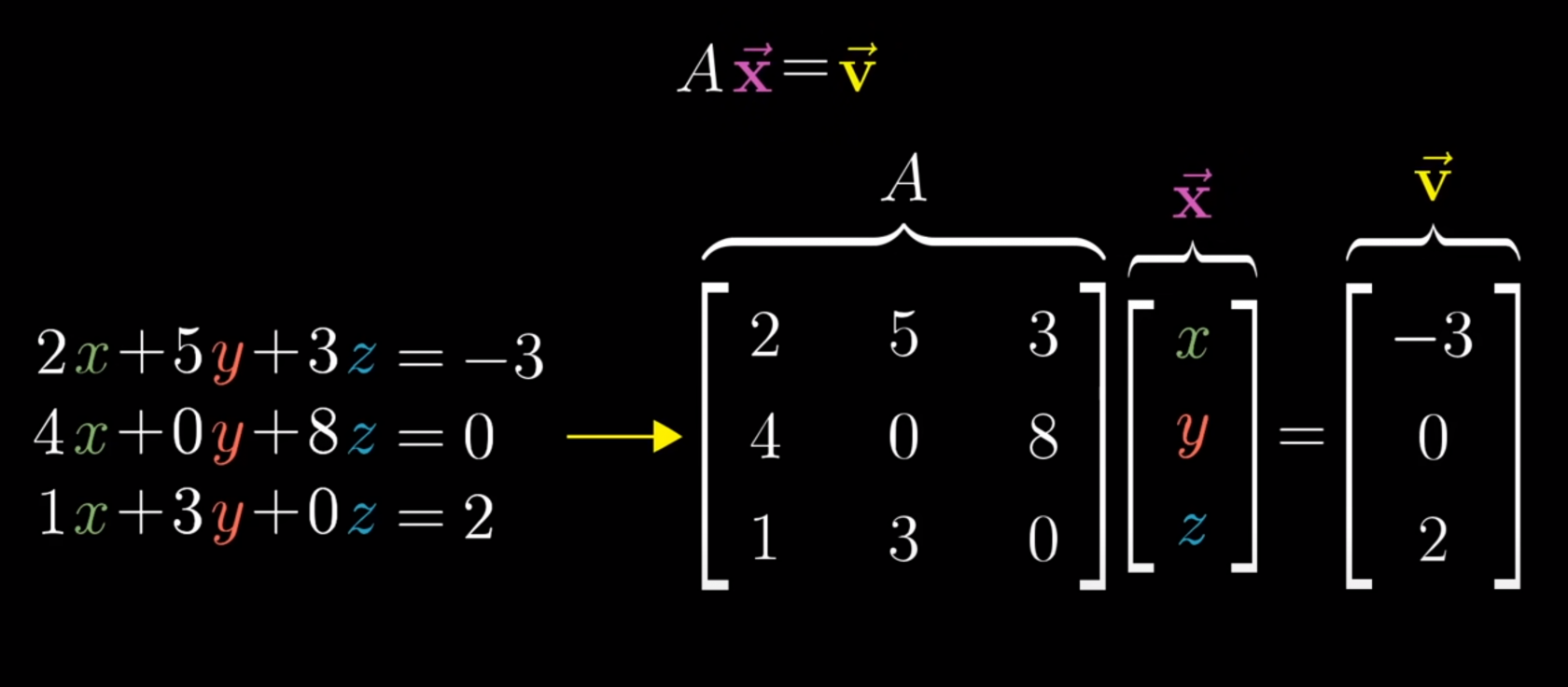


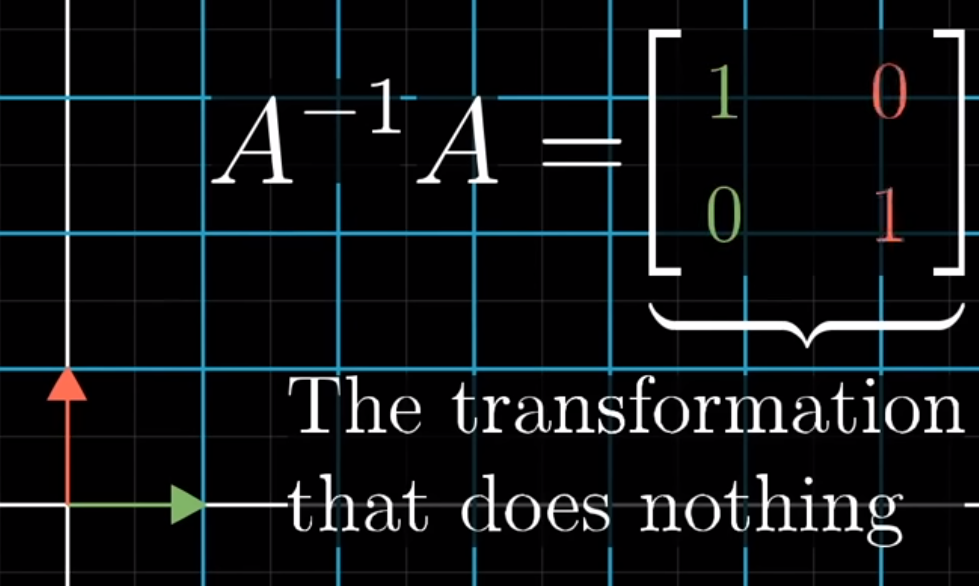
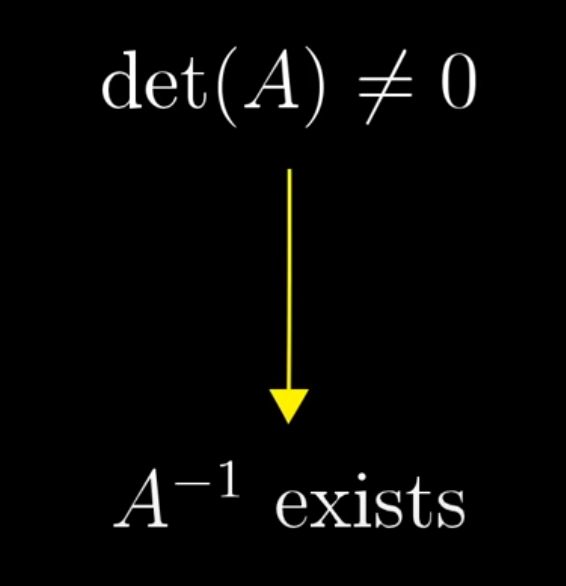

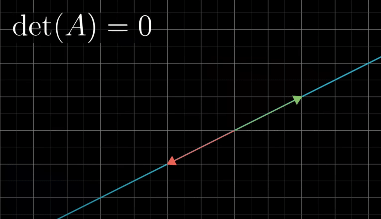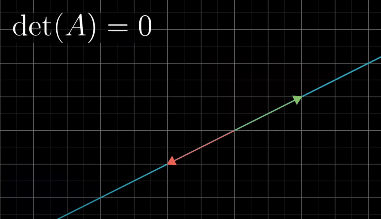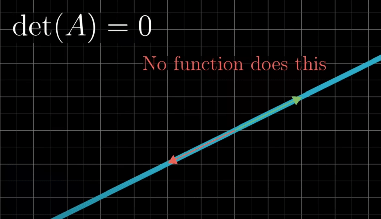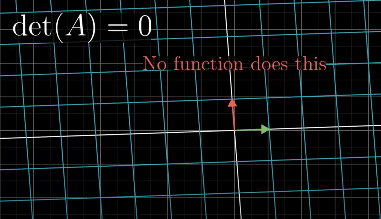
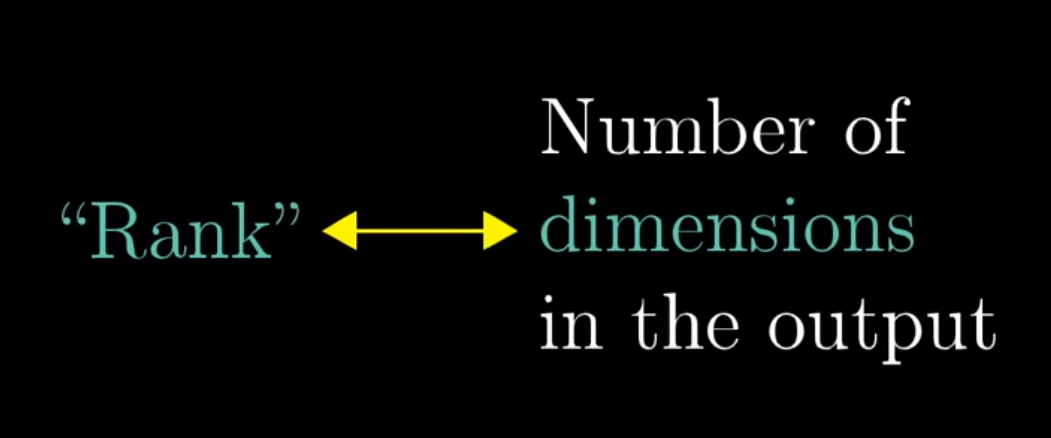




No Comments